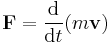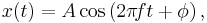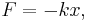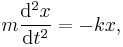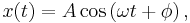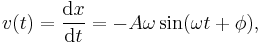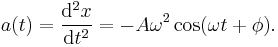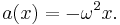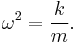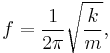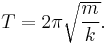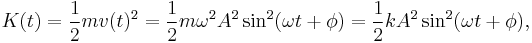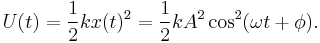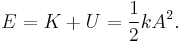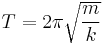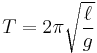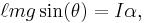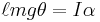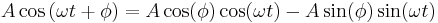Simple harmonic motion

Classical mechanics
History of classical mechanics · Timeline of classical mechanics

In physics, simple harmonic motion (SHM) is the motion of a simple harmonic oscillator, a periodic motion that is neither driven nor damped. A body in simple harmonic motion experiences a single force which is given by Hooke's law; that is, the force is directly proportional to the displacement x and points in the opposite direction.

The motion is periodic: the body oscillates about an equilibrium position in a sinusoidal pattern. Each oscillation is identical, and thus the period, frequency, and amplitude of the motion are constant. If the equilibrium position is taken to be zero, the displacement x of the body at any time t is given by

x(t) = A\cos\left(2\pi\!f t+\phi\right),

where A is the amplitude, f is the frequency, and φ is the phase.

The frequency of the motion is determined by the intrinsic properties of the system (often the mass of the body and a force constant), while the amplitude and phase are determined by the initial conditions (displacement and velocity) of the system. The kinetic and potential energies of the system are also determined by these properties and conditions.

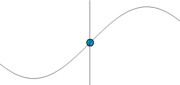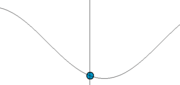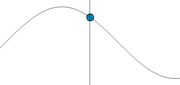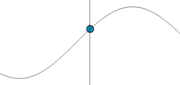
Simple harmonic motion. In this moving graph, the vertical axis represents the coordinate of the particle (x in the equation), and the horizontal axis represents time (t).

Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Other phenomena can be approximated by simple harmonic motion, including the motion of a pendulum and molecular vibration.

Simple harmonic motion provides the basis of the characterization of more complicated motions through the techniques of Fourier analysis.

Contents

Introduction

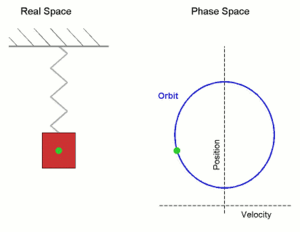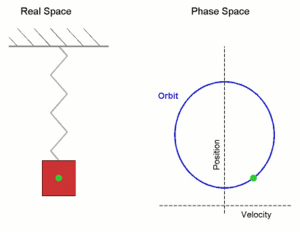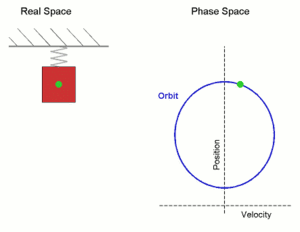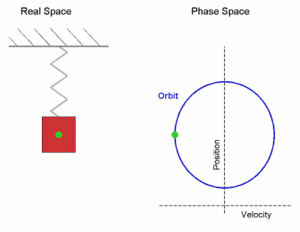
Simple harmonic motion shown both in real space and phase space. The orbit is periodic. (Here the velocity and position axes have been reversed from the standard convention in order to align the two diagrams)

A typical example of a system that undergoes simple harmonic motion is an idealized spring–mass system, which is a mass attached to a spring. If the spring is unstretched, there is no net force on the mass (that is, the system is in mechanical equilibrium). However, if the mass is displaced from equilibrium, the spring will exert a restoring force, which is a force that tends to restore the mass to the equilibrium position. In the case of the spring–mass system, this force is the elastic force, which is given by Hooke's Law,

F = -kx,

where F is the restoring force, x is the displacement, and k is the spring constant.

Any system that undergoes simple harmonic motion exhibits two key features.

  1. When the system is displaced from equilibrium there must exist a restoring force that tends to restore it to equilibrium.
  2. The restoring force must be proportional to the displacement, or approximately so.

The spring-mass system satisfies both.

Once the mass is displaced it experiences a restoring force, accelerating it, causing it to start going back to the equilibrium position. As it gets closer to equilibrium the restoring force decreases; at the equilibrium position the restoring force is 0. However, at x = 0, the mass has some momentum due to the impulse of the force that has acted on it; this causes the mass to shoot past the equilibrium position, in this case, compressing the spring. The restoring force then tends to slow it down, until the velocity reaches 0, whereby it will attempt to reach equilibrium position again.

As long as the system does not lose energy, the mass will continue to oscillate like so; thus, the motion is termed periodic motion. Further analysis will show that in the case of the spring-mass system the motion is simple harmonic.

Dynamics of simple harmonic motion

For oscillation in a single dimension, combining Newton's second law (F = m d2x/dt2) and Hooke's law (F = −kx, as above) gives the second-order linear differential equation

m\frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = -kx,

where m is the mass of the body, x is its displacement from the mean position, and k is a constant.

The solutions to this differential equation are sinusoidal; one solution is

x(t) = A\cos\left(\omega t + \phi\right),

where A, ω, and φ are constants, and the equilibrium position is chosen to be the origin.[A] Each of these constants represents an important physical property of the motion: A is the amplitude, ω = 2πf is the angular frequency, and φ is the phase.[B]

Position, velocity and acceleration of a harmonic oscillator

Using the techniques of differential calculus, the velocity and acceleration as a function of time can be found:

v(t) = \frac{\mathrm{d} x}{\mathrm{d} t} = - A\omega \sin(\omega t+\phi),
a(t) = \frac{\mathrm{d}^2 x}{\mathrm{d}t^2} = - A \omega^2 \cos( \omega t+\phi).
Position, velocity and acceleration of a SHM as phasors

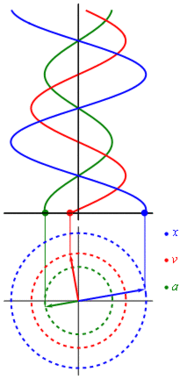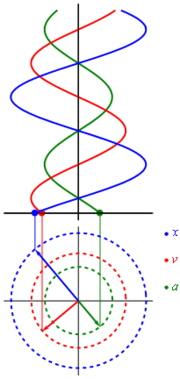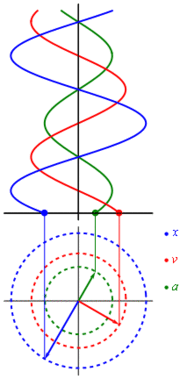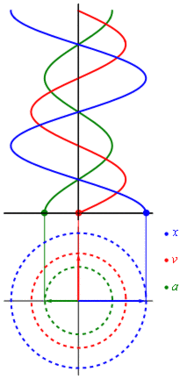
Acceleration can also be expressed as a function of displacement:

a(x) = -\omega^2 x.\!

Now since ma = −mω2x = −kx,

\omega^2 = \frac{k}{m}.

Then since ω = 2πf,

f = \frac{1}{2\pi}\sqrt{\frac{k}{m}},

and since T = 1/f where T is the time period,

T = 2\pi\sqrt{\frac{m}{k}}.

These equations demonstrate that period and frequency are independent of the amplitude and the initial phase of the motion.

Energy of simple harmonic motion

The kinetic energy K of the system at time t is

K(t) = \frac{1}{2} mv(t)^2 = \frac{1}{2}m\omega^2A^2\sin^2(\omega t + \phi) = \frac{1}{2}kA^2 \sin^2(\omega t + \phi),

and the potential energy is

U(t) = \frac{1}{2} k x(t)^2 = \frac{1}{2} k A^2 \cos^2(\omega t + \phi).

The total mechanical energy of the system therefore has the constant value

E = K + U = \frac{1}{2} k A^2.

Examples

An undamped spring-mass system undergoes simple harmonic motion.

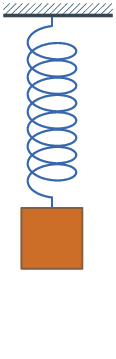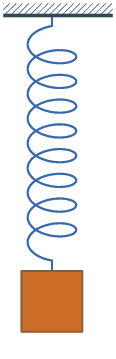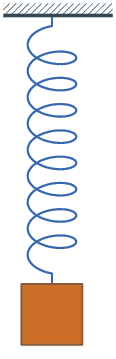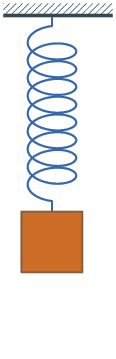
Simple harmonic motion is exhibited in a variety of simple physical systems and below are some examples.

Mass on a spring

A mass m attached to a spring of spring constant k exhibits simple harmonic motion in space. The equation

T= 2 \pi \sqrt{\frac{m}{k}}

shows that the period of oscillation is independent of both the amplitude and gravitational acceleration.

Uniform circular motion

Simple harmonic motion can in some cases be considered to be the one-dimensional projection of uniform circular motion. If an object moves with angular velocity ω around a circle of radius r centered at the origin of the x-y plane, then its motion along each coordinate is simple harmonic motion with amplitude r and angular frequency ω.

Mass on a simple pendulum

The motion of an undamped Pendulum approximates to simple harmonic motion if the amplitude is very small relative to that of the rod.

In the small-angle approximation, the motion of a simple pendulum is approximated by simple harmonic motion. The period of a mass attached to a string of length ℓ with gravitational acceleration g is given by

T = 2 \pi \sqrt{\frac{\ell}{g}}

This shows that the period of oscillation is independent of the amplitude and mass of the pendulum but not the acceleration due to gravity (g), therefore a pendulum of the same length on the Moon would swing more slowly due to the Moon's lower gravitational acceleration.

This approximation is accurate only in small angles because of the expression for angular acceleration being proportional to the sine of position:

\ell m g \sin(\theta)=I \alpha,

where I is the moment of inertia; in this case I = m ℓ 2. When θ is small, sin θ ≈ θ and therefore the expression becomes

\ell m g \theta=I \alpha

which makes angular acceleration directly proportional to θ, satisfying the definition of simple harmonic motion.

See also

Notes

  1. ^ The choice of using a cosine in this equation is arbitrary. Other valid formulations are:
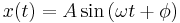    x(t) = A\sin\left(\omega t +\phi\right),
    since cos(θ) = sin(π/2 - θ), or
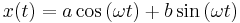    x(t) = a\cos\left(\omega t\right) + b\sin\left(\omega t\right),
    for appropriately chosen constants a and b, derived using the trigonometric identity
    A\cos\left(\omega t +\phi\right) = A\cos(\phi)\cos(\omega t)-A\sin(\phi)\sin(\omega t)
  2. ^ The maximum displacement (that is, the amplitude), xmax, occurs when cos(ωt + φ) = 1, and thus when xmax = A.

External links